Blog 4: Graphical User Interfaces with Matlab, Gamblers Ruin, and Fourier Series
The following are some simple projects I did for fun. The first is a graphical user interface or (GUI), using MatLab. I was interested in GUIs for a while, and glad I finally got around to making my own. However for the MatLab GUI to run the host pc needs to install the MatLab Runtime Compiler (MCR) it is similar to installing Java to run web applications. For that reason and because MatLab is proprietary I am looking into options for my next GUI that utilizes open source software such as Python, GTK+, and Unity.
The GUI below is an application I created in a class called engineering service learning. Our professor wanted to have more computational parts in the lab sessions for the Strength of Materials course, my GUI met that goal. The GUI focuses on solving the deflection of a cantilever beam with fixed boundary conditions at the ends. The shape can be a circle, a rectangle, or a custom shape. The deflection is calculated by solving the second order ODE. Since it only uses the well known second order ODE it is only a valid approximation for small deflections. It is still fun to play with the settings though. Hope you like it! :)
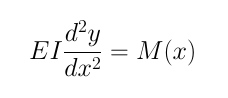
Here is a flyer for an event we had in engineering service learning. Our logo was the coolest out of all the other teams. Actually I believe we were the coolest, most down to Earth and the funnest service learning team. Go IL1!

The simulation here is my spin on the classical gamblers ruin problem. In the gamblers ruin problem a player starts with a certain amount of money and there is a probability that he loses or gains money each turn. The task then is to estimate the probability the player loses all their money (and how fast) or if they reach an upper limit and decide its time to cash out. Here I computationally investigated the probability of winning at the gamblers ruin problem given different starting and ending values. Then visualized the results in 3D.
This video shows an implementation of Fourier series to approximate a piece-wise function. The feature that was of interest to me was the jump at the discontinuity known as the Gibbs Phenomenon and is approximately 9% over and undershoot of the jump discontinuity.